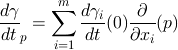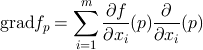接空間とベクトル場

　ＰＤＦ　｜接空間と微分｜ベクトル場｜ベクトル束との関連

　微分と聞くと高校生の時にさんざん計算した思い出か、大学の微分積分学で高次の関数の偏微分を習ったことを思い出すかもしれない。それらの概念を多様体に拡張する。　
　関数の微分係数が、幾何的な意味合いでは接線の傾きに対応していたことを踏まえると、微分という概念は曲がった空間を局所的にまっすぐな空間で近似することを意味しているように感じる。そのまっすぐな空間が接空間である。この定義は一見すると複雑に見えるが、高校生で習った微分を根底に見据えながら読み解くと理解しやすいのかもしれない。結局、点pにおける微分係数の対応というのはpの近傍で定義された関数に対しf → f'(p) という対応である。つまり、関数に対して値を対応させるのである。
　接空間の定義としては、曲線の速度微分によって与えるが、結局それはi方向の偏微分∂/∂xiらによって張られるベクトル空間と一致することに気付く。さらに考察すると、接空間の元（接ベクトル）は上記のような関数環上の線形写像であって、積に関してLipnitz公式を満たすものと一致する。このような写像はderivationと呼ばれ、代数学でもよく見かける。
　多様体間の滑らかな写像 f : M → N があり、f(p)=qとする。ここから接空間上の線形写像df : TpM → ＴqN が導かれる。これが写像fの微分と呼ばれるものである。私たちは今まで、N=RでM=RかR^2ぐらいの場合でこの微分を計算してきた。
　
Mの任意の点pに対し、接ベクトル Xp∈TpMへの対応XをMのベクトル場と呼ぶ。例えば、γ : (-a,a)→ M で、γ(0)=pというような滑らかな曲線を考えたとき、

というγの各成分でt=0での速度微分を係数としてベクトル場が考えられる。また、f : M → Rという滑らかな関数があった場合、

は、fの勾配（gradient）と呼ばれるベクトル場である。勾配という意味は、grad f(f) ≧ 0となっていて、これはつまり、fが増加する方向を向いているベクトル場という意味だからである。接空間やベクトル場については、【松本88】に書かれている。

　接空間やベクトル場の言葉をベクトル束の言葉で説明すると、非常に簡潔になる場合もある。【服部89】を読めばよいと思う。例えば、接空間からは接バンドルという多様体上のベクトル束が考えられ、ベクトル場はこの切断に他ならない。また、多様体にRiemman計量が与えられた場合、勾配ベクトル場は、x∈TMに対し、df(x)=<grad f, x>を満たすものと思えて計算が非常に楽になる。